FP2～3級試験向け!ライフプランニングと資金計画1

今回から複数回に分けてFP試験問題を解けるように内容を解説してまいります。また、問題演習もできるようにしてまいります。

ライフプランニングと資金計画

この範囲では以下のような事柄が問われます。

非常に多岐にわたりますが、過去問的には問われる内容は似たものが多いです。3級では非常に簡単ですが、2級以降ではやや細かな知識が問われるようになります。

2級以上のFP検定を考えている人は、数値などの細かいところも押さえるようにしましょう。

一度に紹介するには範囲が広いので複数回に分けて解説します。

職業倫理

FPは顧客のとてもプライベートな資金に関係する情報を扱うため、厳しく職業倫理を守っていかなくてはいけません。以下の二点が必須になります。

• 顧客利益の優先
• 守秘義務の遵守

FPは他の職業と一部似た内容を取り扱います。この際、他職種の関連業法に抵触してしまうのはダメです。したがって、FPが出来る仕事の範囲と他職種のできる範囲は抑える必要があります。

• 税理士法
• 弁護士法
• 保険業法
• 金融商品取引法

簡単に説明すると、上記の仕事内容のうち、具体性を持つ内容はFPには出来ません。例えば、所得額を聞いて、確定申告の書類を作ってはいけません。一方、給与額から一般的な所得税額等の提示はOKです(年にx万円稼いだら、控除はこの程度で税金はこの程度という分にはOK)。

他に具体的な法律相談や、保険の募集、投資助言はアウトです。FPに可能なのは一般的な情報提供です。

これらを遵守したうえで、顧客の情報を収集する必要があります。

顧客の情報

顧客情報には以下のようなものがあります。

• 収支
• 家族構成
• 顧客（顧客家族）の価値観
• 健康

これらの情報をもとに、どのようなライフイベントが起きるか、将来的な収支、預貯金はどの程度になるのかを決めていきます。この際、顧客の価値観をもとに、アドバイスするように気を付けましょう。FPの意見を押し付けないようにする必要があります。

例えば、趣味の時間を十分に取りたい人に、将来的な資産計画のために趣味の時間を0にしろなどという提案は、資産形成には有益かもしれませんが、顧客利益になっているとは言い難いですね。顧客第一主義がベストでしょう。

顧客情報の分類

顧客情報は大きく分けて２つあります。

顧客情報の利用

ライフイベント表は将来の予定を時系列に表すもの。出産予定など、将来の予定等も含めて記載する。

キャッシュフロー表はライフイベントと合わせて将来の収支や貯蓄残高を計算し表としたもの。FP試験では実技で計算問題が出てくるので、過去問を必ず見ておくこと。

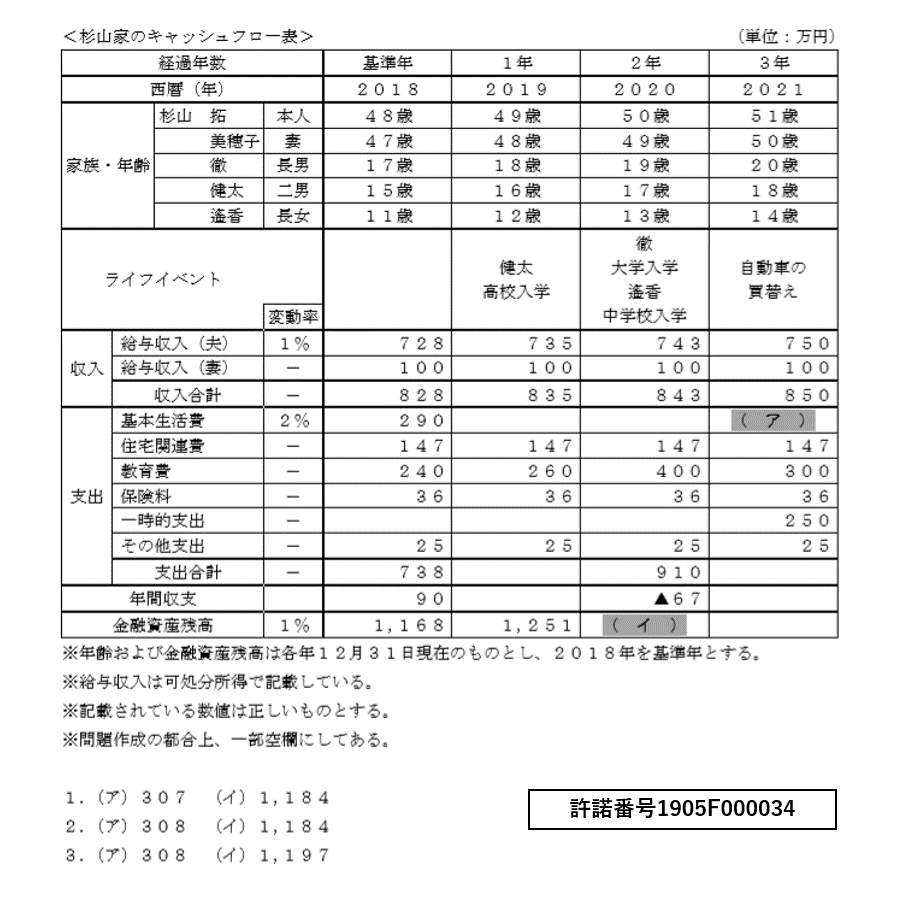
この際、FP試験では可処分所得に関して聞かれることがあります。可処分所得は以下の計算方法でわかります。

可処分所得＝給与等の個人所得　ー　税金　ー　社会保険料

いわゆる手取りのこと。生命保険料などの控除は別で計算します。

貯蓄残高は前年の残高に利率をかけて、運用益もプラスして記載します。現在は利率がほぼゼロなので、実務的には増やせませんが、問題になるときは1%で計算することが多いです。問題に従ってください。

変動率にも従って年々変わることに注意です。

個人のバランスシート

バランスシートとは貸借対照表のことを指し、財務諸表の一つです。ざっくりいうと、資産と負債の状況を一目でわかる表にまとめたものです。

一般的には会社の経営状態などを知るために使われますが、FP的には個人がどの程度の負債を持ち、資産をどの程度持っているのか、を知るために利用します。また、このバランスシートをもとに、老後や、教育資金の準備の仕方を考えます。

純資産＝資産ー負債

ライフプランニングに必要な係数

こちらは試験頻出ですが、覚えるのが大変なもので以下の6種類があります。覚えても表がないと使えないので、各係数がどんな意味を持つのか、また、どのような計算に使われるかを押さえましょう。

• 終価係数
• 現価係数
• 年金終価係数
• 減債基金係数
• 資本回収係数
• 年金現価係数

終価係数は現在の資金を複利運用した際の、将来金額を計算するもの。

現価係数は複利運用で目標額を得るための元本を計算するもの。

年金終価係数は、毎年一定額の複利運用で積立た際の将来額を計算するもの。

減債基金係数は目標額に対する積立額を計算するもの。

資本回収係数は原資を複利運用しながら受け取る額の計算や借入額の返済額を計算するもの。

年金現価係数は、一定期間複利運用しながら、固定金額を受け取るための原資を計算するもの。

この係数は非常に重要ですが、わかりにくいものです。

係数については別ページにて例を提示しながら解説します。