FP知識！６種の係数を覚えよう！

今回は先日予告したFP試験にも頻出の６種の係数についての解説を行います。

使いこなせれば、様々な計算が簡単にできるようになります。また、FP試験で、計算問題が出ることもありますので、使い方を覚えておきましょう。

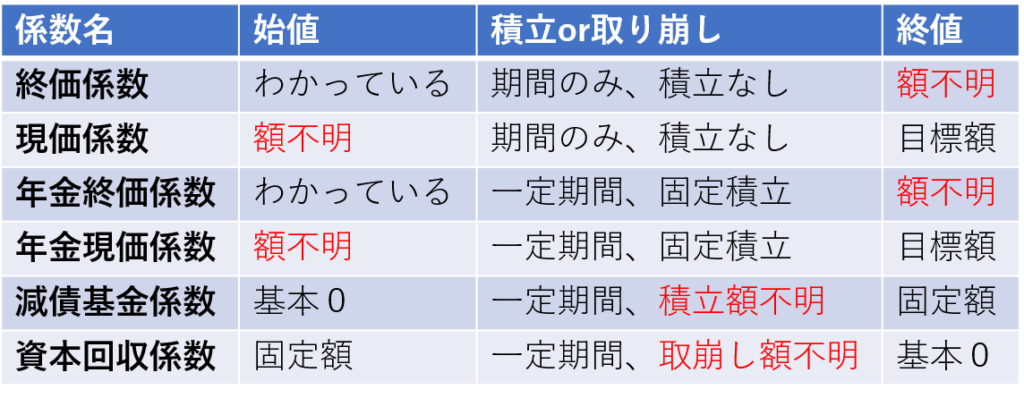
当ページは良く見られていますので、まとめを先に載せておきます。

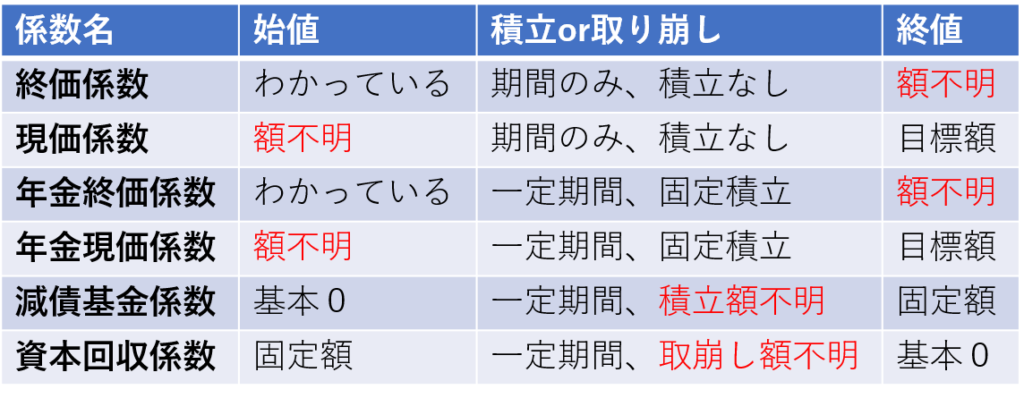
「現」とつくものは目標値を達成するための現在の価格を求めるのに使用し、「終」とつくものは額を固定して進めていった際の期間最終時点の額がわかります。「年金、基金、資本」とつくようなものは一定期間積み立てます。特に、「現」「終」が付かないものは積立額を計算するのに用います。実際問題として、資本回収係数の場合は取り崩す金額と言えます。

積立・取崩し額を計算する係数の場合、積立は初期値0、取崩しでは初期値最大なので、期間中の積立・取崩し額は、取り崩す方が値が大きくなるので、資本回収係数と、減債基金係数が並んでいる場合、取崩しの係数の方が大きいです。

したがって、取崩しは大きい方の値、積立は小さい方の値として判断することも可能です。

６種の係数のおさらい

６種の係数を見てみましょう。

以上の６種類があります。

単語から見ていきましょう。

終価と現価

係数のうち終価とつくものが二つ、現価とつくものが二つあります。それぞれには意味があります。この意味を覚えておくと、係数を覚えるのが楽になります。

まず、終価係数ですが、複利運用した際の将来の金額を計算するときに用いる係数です。

期間と現在価値がわかっている場合に将来どの程度になるのかを計算するときにつかう係数です。将来の不明額を計算するのが終価です。

積立の有無で二種類存在します。

積み立てるものは「年金」とつきます。

反対に現価係数とは将来の金額と期間を固定して複利運用していった際に、現時点での元本がどの程度必要かを計算するものです。つまり現在が不明額になっています。こちらも積立の有無で二種類存在します。

年金～

年金とつくものも二つあります。年金現価係数と、年金終価係数です。現価係数と終価係数はそれぞれ、現在価値が不明か、終値が不明かのいずれかでした。年金～の意味が分かれば、３単語で４つの係数を理解することができます。

年金～とは「一定期間、一定額積立、複利運用」した際の係数を計算します。つまり、年金現価係数とは、「一定期間、一定額積立、複利運用していく際の現在不明額」を計算する際に使用します。一方、年金終価係数は「一定期間、一定額積立、複利運用していく際の将来不明額」を計算することができます。

減債基金係数と資本回収係数

減債基金係数と資本回収係数は、現価、終価とは違って、間の金額を計算するものです。

少しわかりにくいかもしれません、もう少し解説しましょう。

減債基金係数は、期間と目標額（終値）、複利率がわかっている状態で、積み立てる額を計算します。年金終価係数で「一定額」としていた積立額を計算するものです。

一方、資本回収係数は期間と現在価格、複利率がわかっている際に、取り崩していける金額を計算します。こちらは減債基金係数と反対で、年金現価係数で「一定額」としていた部分を計算するものです。

表現が現価、終価でなくてわかりにくいのですが、資本回収係数は借入額の返済の計算にも使えます。そこで、現在の借金を一定期間で返済する際の「一定額」を計算する。つまり借金を回収されると覚えましょう。借金も資本の一つです。

６つの係数を紹介してきました。覚えられたでしょうか？

FP試験ではこれらの係数を用いて計算問題が出題されます。しっかり覚えて計算できるようにしましょう。以下にまとめます。いずれの係数も一定期間中は特定の利率で複利運用されます。積立の有無、求めたい値で使う係数が決まります。

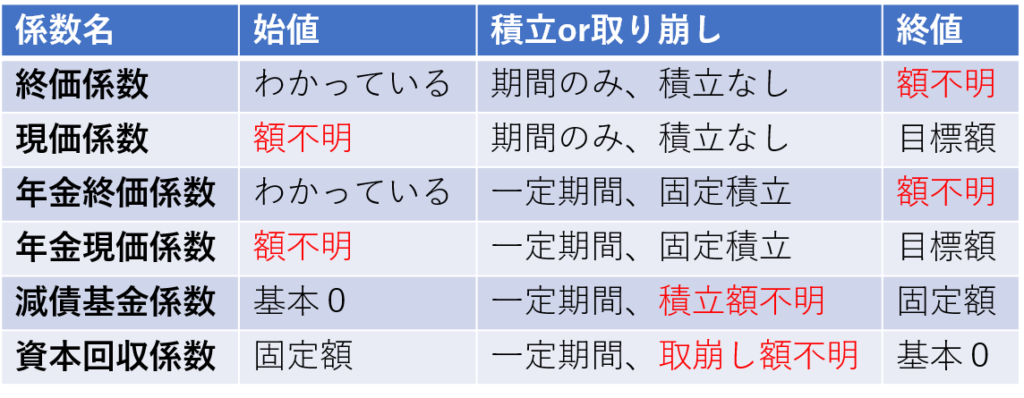
使い方を見てみよう！

試験では係数は与えられます。

過去問を見ていきましょう。（2級、2019年9月）

落ち着いて係数の値を見れば、増えているかどうかや、増加具合から何を求める係数か考えることができます。

時間経過で増えるものは積立額を固定しているか、将来の価格を計算します。

一方、時間経過で減少するものは、現在の価格を計算するか、積立、取崩し額を計算します。

問26は、目標額1500万円がわかっていて、現在額がわからず、積み立てないので、現価係数を使用します。よって、

15,000,000　×　0.951（1%年利、5年の現価係数）　＝　14,265,000

と計算できます。

問27は、15年後の終値がわからず、現在価格０、年60万円積立ですので、年金終価係数を使います。よって、

600,000　×　16.097（1%年利、15年の年金終価係数）　＝9,658,200

と計算できます。

問28は、目標額800万円がわかっていて、現在価格０、期間10年がわかっていて、積立額を求めたいので、減債基金係数を用います。よって

8,000,000　×　0.096（1%年利、10年の減債基金係数）　＝　768,000

と計算できます。

すぐには覚えられないかもしれませんが、覚え方を身につけて、数回使えば大丈夫だと思います！

しっかり覚えましょう！

FP試験では電卓を持ち込めます。安物で良いので買っておきましょう。むしろ高機能だと使用が許されていません。

シャープ カラーデザイン電卓 10桁表示 レッド系 EL-M335-RX 新品価格 ￥742から (2019/12/14 12:33時点)