本日は統計の基礎の中でもグラフについて考えてみましょう。
正規分布
正規分布とは平均値が最も多く、平均値から離れた値になるにつれて、サンプル数が減少していくような形状の分布を言います。下図のようなものです。
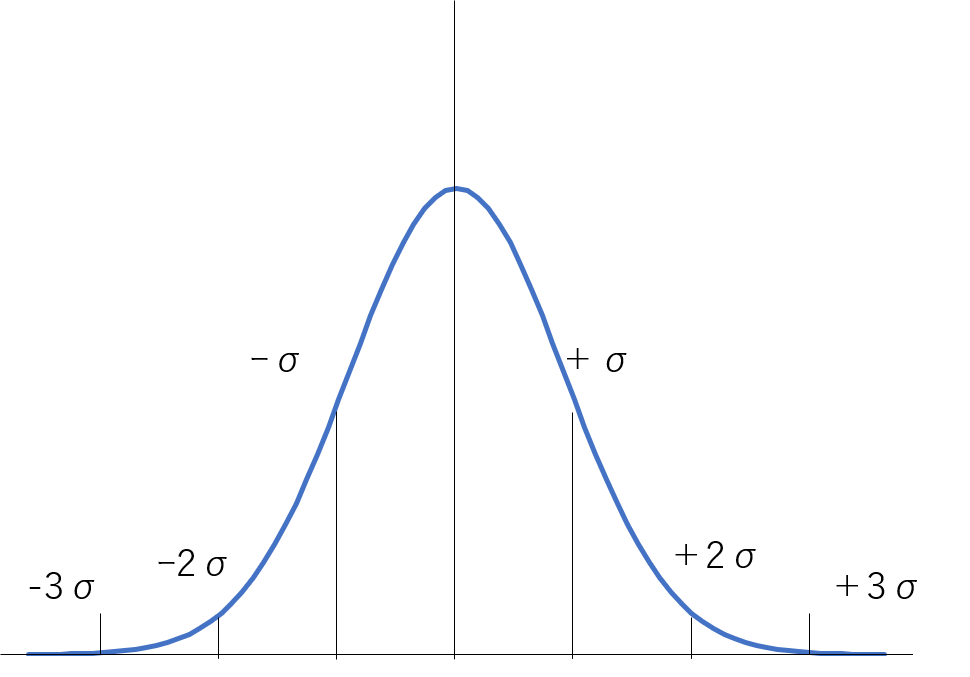
偏差値的な考え方でいうなら平均が50、+σの点数では偏差値60、 +2σなら偏差値70です。
正規分布する場合には標準偏差σと以下のような関係があります。
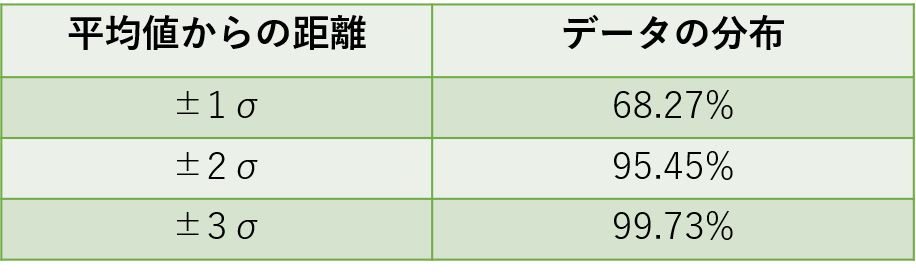
つまり、試験を受けた人が100人いたとして、成績が正規分布していた場合、偏差値40以上60以下の人は約68人いて、偏差値30以上70以下には95人が収まるということです。偏差値が70超えている人は100人中2~3人しかいません。同時に偏差値30以下の人も2~3人だと見積もられます。
気を付けなければならないのは正規分布をしている場合にしか、この分布をしません。例えば、英語のような科目は得意な人と苦手な人で二つの山を持つ点数の分布になることがありますが、そういったケースでは標準偏差は役に立ちません。
投資をする際には期待値が平均値として考えられて、変動リスクをσで見積もることが出来ます。例えば期待値5% 標準偏差±5%の投資商品は損失を出さない確率68.27%となります。ただし、確率がばらつくため単年度での期待値を見積もることしかできません。複利の場合はやや複雑になります。